티스토리 뷰
1. 우선순위 큐 (Priority Queue)

- 우선순위 큐는 일반적인 큐(선입선출, First In. First Out)와 다르게 먼저 들어오는 데이터가 아니라, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조입니다.
- 여러 데이터 중 가장 우선순위가 높은 데이터에 대한 빠른 갱신과 접근이 가능할 때 사용합니다.
- 일반적으로 Heap 구조로 구현하며, 배열과 연결리스트로도 구현이 가능합니다.
배열과 연결 리스트는 간단히 구현이 가능하지만 데이터 삽입의 경우 모든 인덱스를 탐색해야하는 최악의 경우 선능이 좋지 않을 수 있으며, Heap은 구현은 배열과 연결리스트에 비해 어렵지만 좋은 선능을 가집니다.
배열, 연결리스트의 시간복잡도 [ 삽입 : O(n) , 삭제 : O(1) ]
Heap의 시간복잡도 [ 삽입 : O(logN) , 삭제 : O(logN) ]
* Heap?
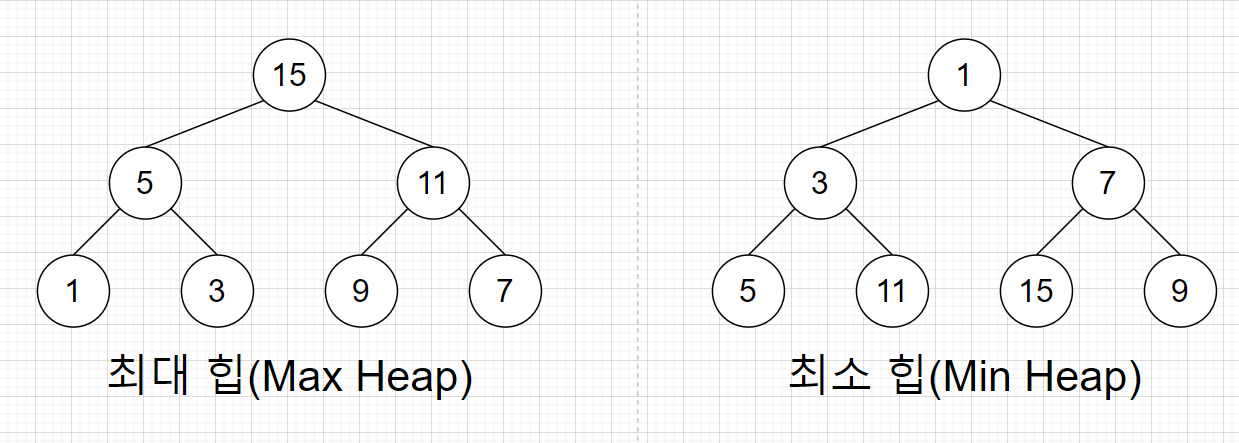
- Heap은 완전 이진 트리이며,( 마지막 레벨을 제외한 모든 레벨의 노드가 완전히 채워져 있으며, 마지막 레벨의 노드는 왼쪽부터 채워져있는 트리 구조) 루트 노드가 최대값을 가지는 최대 힙, 최솟값을 가지는 최소 힙이 있습니다.
- Heap의 인덱스 관계는 아래와 같습니다.
- 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1
- 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 + 2 + 2
- 부모 노드의 인덱스 = Math.floor( ( 자식 노드의 인덱스 - 1 ) / 2 )
2. 우선순위 큐 구현 - JS
2-1. 배열을 통한 구현
class PriorityQueue {
constructor() {
this.queue = [];
}
// 데이터의 우선순위에 따라 큐의 적절한 위치에 삽입
enqueue(element) {
/*
[ array.splice(start[, deleteCount[, item1[, item2[, ...]]]]) ]
- start : 배열의 변경을 시작할 인덱스
- deleteCount : 배열에서 제거할 요소의 수
- item1, item2, ... : 배열에 추가할 요소
*/
for (let i = 0; i < this.queue.length; i++) {
if (this.queue[i] < element) {
this.queue.splice(i, 0, element);
return;
}
}
// 큐에 자신보다 더 작은 값이 없으면, 맨 마지막에 삽입
this.queue.push(element);
}
// 삭제
dequeue() {
return this.queue.shift();
}
front() {
return this.queue[0];
}
size() {
return this.queue.length;
}
clear() {
this.queue = [];
}
}
let pq = new PriorityQueue();
pq.enqueue(3);
pq.enqueue(10);
pq.enqueue(5);
console.log(pq); // => 현재 queue: [ 10, 5, 3 ]
console.log(pq.dequeue()); // => 현재 queue: [ 5, 3 ]
console.log(pq.front()); // = 5
console.log(pq.size()); // = 2
console.log(pq.clear()); // // => 현재 queue: [ ]2-2. Heap을 통한 구현
class PriorityQueue {
constructor() {
// 각 노드별 idx 접근을 쉽게하기 위해 1-based 인덱스를 만들기위해 쓰지않는 값인 0읗 넣어줌
this.queue = [0];
}
enqueue(element) {
let isertIdx = this.queue.length; // 새로운 원소가 삽입될 idx
/*
부모 노드의 값 : Math.floor(qSize / 2);
만일 부모노드의 값이 현재 입력될 값보다 같거나 작으면 부모노드의 값을 isertIdx에 넣어주고
isertIdx를 부모노드의 idx로 바꿔주고 다시 검사
isertIdx > 1 큰 경우에만 isertIdx==1 인 경우는 이미 전체 탐색이 완료한 경우이므로 종료
탐색 후 나온 isertIdx값에 새로운 원소를 넣어주면 됨.
*/
while (isertIdx > 1 && this.queue[Math.floor(isertIdx / 2)] <= element) {
this.queue[isertIdx] = this.queue[Math.floor(isertIdx / 2)]; // 새로운 원소가 삽입될 idx에 부모의 값 넣어주고
isertIdx = Math.floor(isertIdx / 2); // 새로운 원소 삽입 idx를 부모 idx로 바꿔주고 재 검사
}
this.queue[isertIdx] = element;
}
dequeue() {
let delValue = this.queue[1]; // 삭제 될 값
let lastValue = this.queue.pop(); // 큐의 마지막 값
this.queue[1] = lastValue; // 삭제 될 위치에 큐의 마지막 값을 넣어줌
let qSize = this.queue.length - 1; //현재 배열에서 값이 들어갈 수 있는 최대 idx
let pIdx = 1; // 탐색을 시작할 부모idx
let cIdx = 2; // 탐색을 시작할 자식idx
while (cIdx <= qSize) {
// 두 자식중 큰 노드와 부모 노드와 비교
if (this.queue[cIdx] < this.queue[cIdx + 1]) {
cIdx += 1;
}
// 만약 자식 노드와 비교해서 크다면 더이상 검사할 필요가 없으므로 break
if (lastValue >= this.queue[cIdx]) {
break;
}
/*
만약 자식노드가 더 큰 경우 !
현재 부모노드 값에 자식 값을 넣어주고
부모 idx를 자식 idx를 바꾸고 자식 idx를 왼쪽 자식 노드idx로 바꿔주고 다시 검사
*/
this.queue[pIdx] = this.queue[cIdx];
pIdx = cIdx; // 검사할 부모노드는 현재 자식 노드 idx로
cIdx *= 2; // 자식 노드의 왼쪽 자식 노드 idx로
}
// 검사 후 나온 pIdx에 lastValue값을 넣어줌
this.queue[pIdx] = lastValue;
return delValue
}
front() {
return this.queue[1];
}
size() {
return this.queue.length - 1;
}
clear() {
this.queue = [0];
}
}
let pq = new PriorityQueue();
pq.enqueue(10);
pq.enqueue(5);
pq.enqueue(3);
console.log(pq); // => 현재 queue: [ 10, 5, 3 ]
console.log(pq.dequeue()); // => 현재 queue: [ 5, 3 ]
console.log(pq.front()); // = 5
console.log(pq.size()); // = 2
console.log(pq.clear()); // // => 현재 queue: [ ]
- 배열, Heap을 이용하여 모두 최대 힙을 구현했습니다. 최소 힙을 구하기 위해선 값을 비교하는 부분만 반대로 수정하면 됩니다!
다른 언어와 달리 JS에서는 우선순위 큐를 기본 제공하는 라이브러리가 없기때문에 알고리즘을 풀 때 직접 구현하여 사용해야한다. 배열로 구현 시 시간 성능에서 좋지 않기때문에 heap으로 구현하는 법에 대해서 공부하는 것을 추천한다! 부모와 자식 노드 간의 idx 관계를 잘 생각해보면 구현하는데 크게 도움이 된다!
🔗 참고한 글
- heap을 이용한 알고리즘 풀이는 아래 블로그글을 참고했으며, 개인적으로 정리가 깔끔해서 보기 좋았다. enqueue, dequeue 동작 과정이 이해가 가지 않으면 아래 블로그에서 사진과 함께 보는 것을 추천 !!
[javascript] 우선순위 큐, heap (2)
heap 이란 ? heap 은 우선순위 큐를 위해서 만들어진 트리자료구조이다. heap은 부모노드와 자식노드의 대소관계에 따라 최대힙(Max heap)과 최소힙(Min heap)으로 나뉜다. heap의 특징 heap은 완전이진트리
hokeydokey.tistory.com
'Algorithm' 카테고리의 다른 글
| [JS] [Programmers] 삼각 달팽이 (0) | 2022.06.17 |
|---|---|
| [JS] [Programmers] [3차] n진수 게임 (0) | 2022.06.17 |
| 알고리즘 풀이에 도움되는 수학 정리 ! (0) | 2022.05.27 |
| 누적합(Prefix Sum / Cumulative Sum) 알고리즘 (0) | 2022.05.24 |
| 슬라이딩 윈도우 알고리즘(Sliding Window) (feat. 투 포인트) (0) | 2022.05.23 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 타입스크립트
- next.js 환경변수
- useRef
- 가상스크롤
- 매겨변수와 인자
- 렌더링 속도 개선
- next.js에 .gitignore가 적용되지 않을 때
- 1급 시민
- 시맨틱 웹
- 자바스크립트 비동기 동작원리
- typescript
- rewrites
- react
- 1급 함수
- React로 쓰로틀링 디바운싱 구현
- redirects
- 함수형 컴포넌트
- javascript
- 자바스크립트 동작원리
- programmers
- 호이스팅
- redux
- debouncing
- Virtual Scroll
- zustand
- Next.js
- array
- vue
- 목표 일기
- 1급 객체
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
